記述幾何学では、表面は、空間内の移動する線または他の表面の連続する位置のセットとして考慮されます。 空間内を移動して面を形成する線を母線と呼びます。 発電機は直線状または曲線状にすることができます。 生成する曲線は、一定にすることも、自然に変化するなどの可変にすることもできます。

多くの場合、同じ表面がさまざまな母線の動きによって形成されると考えることができます。 たとえば、円柱は次のように形成できます。まず、母線に平行な固定軸に対して直線を回転させます。 第二に、円の移動によって、その中心は円の平面に垂直な直線に沿って移動します。 第三に、球体の直線運動によるものです。

図面でサーフェスを描写する場合、母線の多くの可能な位置のうちの一部のみが表示されます。 図では、 8.1 は母線の表面を示しています AB。移動中、母線は方向に対して平行を保ちます。 ミネソタ州そして同時にある曲線を横切る CDE。したがって、母線の動きは、 AB空間を線で導かれて CDE。

サーフェスの形成中に母線の移動の前提条件となる交差する線は、ガイドと呼ばれます。

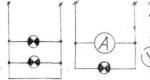
図では、 8.2 は直線の移動によって形成される表面を示しています AB 2 つのガイドに沿って - ストレート O1<⅞ （阿部央私 ○ 2) そして空間曲線 F.G.L.線O1と交差していません 0 2.

場合によっては、母線に特徴的な点 (円の中心など) がその上に移動するガイドとして線が使用されることがあります。

母線、ガイド、および特定の表面の形成パターンのさまざまな形式から、図面で表面を描写し、それに関連する問題を解決するのに最も単純で便利なものが選択されます。

曲面を定義するために、「曲面決定要因」という概念が使用されることがあります。これは、曲面を一意に定義する一連の独立した条件を意味します。 行列式に含まれる条件のうち、幾何学的な部分（点、線、面）と、行列式の幾何学的な部分によって面を形成する法則（アルゴリズム）とが区別される。

記述幾何学で採用される曲面の簡単な分類を考えてみましょう。

罫線入り可展面。直線で形成できる面を線織面といいます。 線織面を、表面に損傷 (破れや折り目) を与えることなく、すべての点が平面と一致するように展開できる場合、その線織面は展開可能であると呼ばれます。 可展面には、隣接する直線母線が平行または交差する線織面、または何らかの空間曲線に接する線織面のみが含まれます。 他のすべてのルールド サーフェスおよびすべての非ルールド サーフェスは、開発不可能なサーフェスとして分類されます。

可展面は円筒形、円錐形で、戻りリブまたは胴部があります。 円筒面では、母線は常に平行であり、ガイドは 1 つの曲線です。 以前に空間内に示した円筒面の図 (図 8.1 を参照) を図に示します。 8.3. 特殊なケースは、真っ直ぐな円柱、傾斜した円柱です (図 9.17 を参照、ガイドは円であり、その平面は円柱の軸に対してある角度で位置し、中心がその軸上にあります)。 円錐面の場合、すべての直線母線には共通の固定点 (頂点、ガイド、いずれか 1 つの曲線) があります。 円錐のイメージ例

図面内の表面 - 図。 8.4、頂点の投影 ぐ、ぐ、ガイド C「D」E、C「D」E。特殊なケース - 真っ直ぐな円錐、傾斜した円錐 - 図を参照してください。 10.10ですね。 リターン エッジまたは胴体を持つサーフェスの場合、直線母線は 1 つの曲線ガイドに接します。

線引き非開発可能サーフェス:円柱、円錐、双曲放物面（斜平面）。 円筒面と呼ばれる面は、すべての位置で特定の平面 (「平行面」) に平行を保ち、2 つの曲線 (2 つのガイド) と交差する直線を移動することによって形成されます。 円錐面と呼ばれる面は、直線を移動することによって形成されます。この直線は、すべての位置で特定の平面 (「平行面」) と平行を保ち、一方は曲線、もう一方は直線である 2 つのガイドと交差します (図) .8.5、図8.2も参照）。 図の平行面です。 8.5 は平面 π1 です。

ガイド - 突起のある曲線 E「G」F、E「G」F、突起のある直線 お、０、お」,0. 特定のケースでは、湾曲したガイドが直線ガイドと一致する軸を有する円筒状の螺旋線である場合、結果として得られる表面は、以下で説明する螺旋状の円錐形となる。 斜平面と呼ばれる双曲放物面の図を図に示します。 8.6. この表面の形成は、特定の平行面に平行な直線を横切る 2 つのガイドに沿った直線母線の移動の結果と考えることができます。 図では、 8.6 平行面 - 投影面 - ガイド - 突起のある直線 も、も、も」そして ファ「ゴ」、ファ「ゴ」。

罫線のない表面。それらは、一定の母線をもつサーフェスと可変母線をもつサーフェスに分割されます。

一定の母線をもつ表面は、次に、球、トーラス、回転楕円体などの曲線母線をもつ回転面と、一定の曲線を描くパイプの表面などの周期曲面に細分化されます。断面、スプリング。

可変母線を持つ曲面は、2 次曲面、可変母線を持つ周期曲面、およびフレーム曲面に細分されます。 2 次曲面 (楕円体) の図を図に示します。 8.7. 楕円体の母線は変形可能な楕円です。 2 つのガイドは 2 つの交差する楕円であり、その平面は直交し、1 つの軸が共通です。 母線は、その軸の端点でガイドと交差します。

移動中、生成される楕円の平面は、ガイド楕円の 2 つの交差軸によって形成される平面と平行のままです。

可変母線を持つ周期的表面には、母線 - 可変半径の円、ガイド - 母線の中心が移動する曲線があり、母線の平面はガイドに垂直です。 フレーム サーフェスは、移動する母線ではなく、サーフェス上の特定の数の線によって定義されます。

通常、このような線は平坦な曲線ですが、

その平面は互いに平行です。 このような線の 2 つのグループが互いに交差し、線織面枠を形成します。 線の交点は、サーフェスの点フレームを形成します。 サーフェスのポイント フレームは、サーフェスの点の座標によって指定することもできます。 フレーム表面は、船体、航空機、自動車、ブラウン管シリンダーの構造に広く使用されています。

このうち、ねじ面について詳しく見ていきます。

- (ρ 1 , T 1 , v → 1 (\displaystyle \rho _(1),T_(1),(\vec (v))_(1)))、右側はその他( ρ 2 , T 2 , v → 2 (\displaystyle \rho _(2),T_(2),(\vec (v))_(2))）。 媒体が不安定に移動する場合、不連続面は静止したままではなく、その速度は媒体の速度と一致しない可能性があります。

物理的に、任意の不連続性は有限時間存在することはできません。これには力学方程式の違反が必要になります。 このため、ある状況で任意の不連続によって記述される状態が発生した場合、その状態はその発生と同時に減衰し始めます。任意の不連続の減衰に関するリーマン問題を参照してください。 この場合、現象が発生する媒体と、不連続の反対側の状態変数の値が互いにどのように関係しているかに応じて、通常の不連続と希薄化波のさまざまな組み合わせが発生する可能性があります。

条項

以下の角括弧は、サーフェスの異なる側面の値の違いを示します。

破断面では特定の関係が満たされる必要があります。

1. 亀裂の表面には材料が連続的に流れていなければなりません。 破面の要素を通過する単位面積当たりのガス流量は、破面の両側で大きさが等しくなければなりません。つまり、次の条件が満たされなければなりません。 [ ρ u x ] = 0 (\displaystyle \left[\rho u_(x)\right]=0)軸方向 x (\表示スタイル x)不連続面に垂直になるように選択されます。
2. エネルギーが継続的に流れている必要があります。つまり、条件が満たされている必要があります。 [ ρ u x (u 2 2 + ε) ] = 0 (\displaystyle \left[\rho u_(x)\left((\frac (u^(2))(2))+\varepsilon \right)\right ]=0)
3. 継続的な運動量の流れが存在し、破断面の両側でガスが互いに作用する力は等しくなければなりません。 法線ベクトルは x 軸に沿っているため、連続性は次のようになります。 x (\表示スタイル x)- 運動量の流れの成分が状態を引き起こす [ p + ρ u x 2 ] = 0 (\displaystyle \left=0) [ ρ u x u y ] = 0 (\displaystyle \left[\rho u_(x)u_(y)\right]=0)そして [ ρ u x u z ] = 0 (\displaystyle \left[\rho u_(x)u_(z)\right]=0)

上の方程式は、不連続面上の境界条件の完全なシステムを表します。 これらのことから、不連続面には 2 つのタイプがあると結論付けることができます。

接線方向の不連続性

破断面を通る物質の流れはありません

( ρ 1 u 1 x = ρ 2 u 2 x = 0 ρ 1 , ρ 2 ≠ 0 ⇒ u 1 x = u 2 x = 0 ⇒ p 1 = p 2 (\displaystyle (\begin(cases)\rho _( 1)u_(1x)=\rho _(2)u_(2x)=0\\\rho _(1),\rho _(2)\neq 0\end(cases))\Rightarrow \qquad u_(1x )=u_(2x)=0\qquad \Rightarrow p_(1)=p_(2))

したがって、この場合、法線速度成分とガス圧力は破断面上で連続します。 接線速度 u z (\displaystyle u_(z)), u y (\displaystyle u_(y))密度がランダムにジャンプする可能性があります。 このような休憩はと呼ばれます 接線方向.

接触ギャップ- 接線方向の不連続性の特殊なケース。 速度は連続的です。 密度はジャンプし、それに伴って圧力を除く他の熱力学量もジャンプします。

衝撃波

2 番目のケースでは、物質の流れとそれに伴う量はゼロではありません。 次に、条件から次のようになります。

[ρ u x ] = 0 ; [ρ u x u y ] = 0 ;そして [ ρ u x u z ] = 0 (\displaystyle \left[\rho u_(x)\right]=0;\qquad \left[\rho u_(x)u_(y)\right]=0;\qquad \left[ \rho u_(x)u_(z)\right]=0)

[ u y ] = 0 (\displaystyle \left=0\quad )

[ u z ] = 0 (\displaystyle \quad \left=0) 接線速度は破断面で連続的です。 密度、圧力、およびそれらとともに他の熱力学量はジャンプを経験し、これらの量のジャンプは関係、つまり不連続条件によって関連付けられます。 [ ρ u x (u 2 2 + ε) ] ; (\displaystyle \left[\rho u_(x)\left((\frac (u^(2))(2))+\varepsilon \right)\right];)

[u y] = 0;

(\displaystyle \left=0;)

[ u z ] = 0 (\displaystyle \left=0)

[ρ u x ] = 0 ;, [ u x 2 2 + ε ] = 0 ;

一次元の非定常の場合のガス力学的不連続性は、平面内の曲線によって幾何学的に表現されます。 このボリュームを囲む輪郭の 2 つの辺が不連続点の両側の不連続点に平行になり、他の 2 つの辺が不連続点に垂直になるように、不連続点の近くにコントロール ボリュームを構築しましょう。 与えられた制御ボリュームのシステムを記述し、辺をゼロに縮小し、これらの辺の積分の値を無視すると、輪郭の横断方向と座標増分の符号を考慮して、次の結果が得られます。不連続部に隣接する側面:

∫ 1 − 2 (q d x − f d t) − ∫ 3 − 4 (q d x − f d t) = 0 (\displaystyle \int \limits _(1-2)(qdx-fdt)-\int \limits _(3-4) (qdx-fdt)=0) ∫ 1 − 2 (q d x d t − f) − ∫ 3 − 4 (q d x d t − f) = 0 (\displaystyle \int \limits _(1-2)(q(\frac (dx)(dt))-f)- \int \limits _(3-4)(q(\frac (dx)(dt))-f)=0)

マグニチュード D = d x d t (\displaystyle D=(\frac (dx)(dt)))- 破壊伝播速度

断絶の関係

長方形の方法と不連続点での量のジャンプの表記法を使用した積分の近似に移り、関係系を取得します。

[ ρ ] D − [ ρ u ] = 0 ; (\displaystyle \left[\rho \right]D-\left[\rho u\right]=0;) [ ρ u ] D − [ p + ρ u 2 ] = 0 ;

(\displaystyle \left[\rho u\right]D-\left=0;)

[ E ] D − [ u (E + p) ] = 0 ;

(\displaystyle \leftD-\left=0;)

例

破断面では特定の境界条件が満たされる必要があります。

これらの条件を定式化するには、不連続面のある要素を考慮し、この要素に関連付けられた座標系を、その要素に垂直に向けられた軸とともに使用します。

まず、破断面には材料が連続的に流れていなければなりません。つまり、一方の面に入るガスの量は、面のもう一方の面から出ていくガスの量と等しくなければなりません。 したがって、考慮中の表面要素を通過するガス流量 (単位面積当たり) は、インデックス 1 と 2 が不連続面の 2 つの側面を指す条件と等しくなります。

以下では、角括弧を使用して、不連続面の両側の量の値の差を示します。 それで、

結果の条件は次の形式で書き込まれます。

最後に、継続的な運動量の流れが存在する必要があります。つまり、破断面の両側でガスが互いに作用する力が等しくなければなりません。 単位面積を通る運動量流束は次の値に等しい (§ 7 を参照)

法線ベクトルは軸に沿った方向を向いているため、運動量の流れの A - 成分の連続性がこの条件につながります。

y 成分と - 成分の連続性により、次のようになります。

方程式 (84.1-4) は、不連続面上の境界条件の完全な系を表します。 これらから、不連続面には 2 つのタイプがあるとすぐに結論付けることができます。

最初のケースでは、不連続面を通る物質の流れはありません。 これは、 がゼロではないので、次のものが存在する必要があることを意味します。

この場合、条件 (84.2) と (84.4) は自動的に満たされ、条件 (84.3) は次のようになります。 したがって、この場合の不連続面では法線速度成分とガス圧力は連続です。

接線方向の速度と密度 (および圧力以外の熱力学量) は、任意のジャンプを経験する可能性があります。 このような不連続性を接線方向と呼びます。

2 番目のケースでは、物質の流れとそれに伴う物質の流れはゼロとは異なります。 次に、(84.1) と (84.4) から次のようになります。

つまり、接線速度は不連続面上では連続です。 密度、圧力 (したがって他の熱力学的量)、および通常の速度はジャンプを経験し、これらの量のジャンプは関係 (84.1-3) によって関連付けられます。 条件 (84.2) では、(84.1) のおかげで減らすことができ、代わりに v の連続性により v と書くことができます。 したがって、検討中のケースの不連続面では、次の条件が存在する必要があります。

このタイプの破壊は衝撃波と呼ばれます。

ここで固定座標系に戻ると、代わりに、不連続面に垂直なガス速度成分と、定義によりその法線に沿った表面自体の速度との差をどこにでも記述する必要があります。

速度 および および は、固定基準フレームを基準にして取得されます。 速度は、破断面に対するガスの移動速度です。 そうでない場合は、ガスに対する破断面自体の伝播速度があると言えます。 この速度は、表面の両側のガスに関して異なることに注意してください (ガスが破裂した場合)。

接線方向の速度成分がジャンプする接線方向の不連続点については、すでに§ 29 で検討しました。そこでは、非圧縮性流体ではそのような不連続点は不安定であり、乱流領域に浸食されるはずであることが示されました。 圧縮性流体に関する同様の研究では、このような不安定性が任意の速度の一般的な場合にも発生することが示されています (問題 1 を参照)。

接線方向の不連続性の特殊なケースは、速度が連続的で、密度 (およびそれに伴って圧力を除く他の熱力学量) のみがジャンプする不連続性です。 このようなギャップは接触と呼ばれます。 不安定性について上で述べたことは、それらには当てはまりません。

ブレイクライン

ブレイクライン

航空機の戦闘経路の線と平行にブレークポイントを通る直線。

サモイロフ K.I. 海洋辞典。 - M.-L.: ソ連 NKVMF の国家海軍出版社, 1941

他の辞書で「BREAK LINE」が何であるかを確認してください。

ギャップを参照してください。 地質辞典: 2 巻。 母：ネドラ。 K. N. パフェンゴルツら編集 1978 ... 地質百科事典

破線- sprogimo linija statusas T sritis Gynyba apibrėžtis Tiesė、jungianti pabuklą su sprogimu。 アティティクメニス：英語。 バーストラスのライン。 改行…Artilerijos terminų žodynas

ウィンドシャーライン- 防風線、風速や風向が異なるゾーンの境界... 風辞典

地層（層、鉱脈などの地質体）の屋根または底面、あるいは破壊面に位置します。 ストライクラインへ。 地層（層、脈）または破断面の窪みに沿って下向きに向けられます。 「秋」を参照してください。 地質辞典: 2 巻。 ま... 地質百科事典

ライン- (1) 2 つの隣接する表面領域の共通部分。 (2) L. 機械と機械、主装置と補助装置の自動複合体であり、プロセス全体を技術的な順序で所定のリズムで自動的に実行します。 ポリテクニック大百科事典

地層（層、鉱脈などの地質体）の屋根や底、または破砕面と水平面との交線。 「ひれ伏す」を参照。 地質辞典: 2 巻。 母：ネドラ。 K. N. パフェンゴルツら編集 1978 ... 地質百科事典

ブレークポイントとリリースポイントを結ぶ直線。 サモイロフK.I.海洋辞書。 M. L.: ソ連 NKVMF の国家海軍出版社、1941 ... 海洋辞典

この記事または記事のセクションには、地下鉄に関連して予想されるイベントまたは計画されているインフラ施設に関する情報が含まれています。 百の内容…ウィキペディア

- (FOCL)、光ファイバー通信回線 (FOCL) は、受動素子と能動素子で構成される光ファイバー システムで、光 (通常は近赤外線) 範囲で情報を送信するように設計されています。 目次 1 ... ウィキペディア

骨折- 骨折、固体物体 (ウェグナー)、この場合は骨の完全性が完全に破壊されること。 P.は最も重度の外傷の結果であり、外傷学の最も深刻な章の1つを構成します。 ブランズの統計によると（ロンドン病院は30万人……） 偉大な医学百科事典

本

• 古典文学をスクリーンで。 Not a Step Back (4DVD)、エルショフ・ミハイル・イワノビッチ、ストルパー・アレクサンダー、エギアザロフ・ガブリイル・ゲオルギエヴィッチ。 1. 封鎖。 PART 1 (1975年、2作品、177分) アレクサンダー・チャコフスキーの同名小説を原作とした大作映画。 VKF賞受賞。 1941 年の夏までに、ファシスト侵略者はレニングラードに接近しました。 のみ…

マタナリシスに関する講義ノート

いくつかの変数の関数。 2 つの変数の関数の幾何学的表現。 レベルの線と面。 いくつかの変数の関数の極限と連続性、その性質。 偏導関数、その性質および幾何学的意味。

定義 1.1.変数 z (チェンジエリアあり Z) 呼ばれた 2 つの独立変数の関数 x、y豊富に M、各ペアの場合 ( x、y) たくさんの方から M zから Z.

定義 1.2.多くの M、変数が指定されています x、y、呼ばれた 関数のドメイン、そして彼ら自身 x、y- 彼女 引数.

指定: z = f(×, y), z = z(×, y).

例。

コメント。いくつかの数字があるので ( x、y) は、平面上の特定の点の座標と考えることができます。その後、「点」という用語を、2 つの変数の関数に対する一対の引数、および順序付けられた数値セットに対して使用します。
、これらは複数の変数の関数への引数です。

定義 1.3. . 変数 z (チェンジエリアあり Z) 呼ばれた いくつかの独立変数の関数
豊富に M、各数値セットの場合
たくさんの人から M何らかの規則または法律に従って、1 つの特定の値が割り当てられます zから Z. 引数とドメインの概念は、2 変数の関数の場合と同じ方法で導入されます。

指定: z = f
,z = z
.

2 つの変数の関数の幾何学的表現。

機能を考えてみる

z = f(×, y) , (1.1)

ある地域で定義されている M O面上で xy。 次に、座標を持つ 3 次元空間内の点のセット ( ×, y, z) ここで、 は 2 つの変数の関数のグラフです。 式 (1.1) は 3 次元空間内の特定の面を定義するため、それが考慮中の関数の幾何学的イメージになります。

z = f(x,y)

M y

コメント。 3 つ以上の変数の関数については、「表面の関数」という用語を使用します。 n「次元空間」を表現することは不可能ですが、そのような表面を描くことは不可能です。

レベルの線と面。

式 (1.1) で与えられる 2 つの変数の関数については、一連の点を考慮できます ( x、y) O面 xy、そのために z 同じ定数値を取る、つまり z= 定数 これらの点は、と呼ばれる平面上に線を形成します。 レベルライン.

例。

サーフェスのレベル ラインを見つける z = 4 – ײ - y²。 彼らの方程式は次のようになります ײ + y² = 4 – c (c=const) – 原点を中心とし半径を持つ同心円の方程式
。 たとえば、次のようなとき と=0 円が得られます ײ + y平方 = 4 。

3 変数の関数の場合 あなた = あなた (×, y, z) 方程式 あなた (×, y, z) = cと呼ばれる 3 次元空間内の表面を定義します。 平らな面.

例。

機能について あなた = 3× + 5y – 7z–12 個の水平面は、次の方程式で与えられる平行面の集合になります。

3× + 5y – 7z –12 + と = 0.

複数の変数の関数の極限と連続性。

コンセプトを紹介しましょう δ近傍ポイント M 0 (× 0 、y 0 ) O面上で xy与えられた点を中心とする半径δの円として。 同様に、3 次元空間内の δ 近傍を、点を中心とした半径 δ のボールとして定義できます。 M 0 (× 0 、y 0 , z 0 ) 。 のために n- 点のδ近傍と呼ぶ次元空間 M 0 ポイントのセット M座標付き
、条件を満たす

どこ
- 点座標 M 0 。 場合によっては、このセットを「ボール」と呼ぶこともあります。 n-次元空間。

定義 1.4.数字Aが呼ばれます 限界いくつかの変数の関数 f
時点で M 0の場合

そのような | f(M) – あ| < ε для любой точки Mδ近傍から M 0 .

指定:
.

この場合のポイントは次のとおりであることを考慮する必要があります。 M近づいているかもしれない M相対的に言えば、点のδ近傍内の任意の軌道に沿った 0 M 0 。 したがって、一般的な意味でのいくつかの変数の関数の極限と、いわゆる限界を区別する必要があります。 繰り返される制限各引数の限界まで連続するパッセージによって個別に取得されます。

例。

コメント。 通常の意味での所与の点での極限の存在と、個々の議論のこの点での極限の存在から、繰り返される極限の存在と平等が続くことが証明できる。 逆の記述は真実ではありません。

定義 1.5.関数 f
呼ばれた 継続的な時点で M 0
、 もし
(1.2)

表記法を導入すると

その条件 (1.2) は次の形式で書き換えることができます。

(1.3)

定義 1.6.内側の点 M 0 機能ドメイン z = f (M) 呼ばれた ブレークポイントこの時点で条件 (1.2)、(1.3) が満たされていない場合に関数を実行します。

コメント。平面上または空間内に多数の不連続点が形成されることがあります 行または 破面.