線形依存行列の列。
テクニカルプレビュー
させて マトリックスの列を次元化します。行列列の線形結合 列行列と呼ばれる、いくつかの実数または複素数を含む線形結合係数
。 線形結合ですべての係数がゼロに等しい場合、線形結合はゼロ列行列と等しくなります。 行列の列は次のように呼ばれます。 線形独立 、線形結合のすべての係数がゼロに等しい場合にのみ、それらの線形結合がゼロに等しい場合。 行列の列は次のように呼ばれます。 線形依存性
、少なくとも 1 つがゼロ以外の一連の数値があり、これらの係数を持つ列の線形結合がゼロに等しい場合
同様に、行列行の線形依存性と線形独立性の定義を与えることができます。 以下では、すべての定理が行列の列に対して定式化されます。
定理5
行列の列にゼロがある場合、行列の列は線形に依存します。
証拠。 すべての非ゼロ列についてはすべての係数がゼロに等しく、すべてのゼロ列については 1 に等しい線形結合を考えてみましょう。 これはゼロに等しく、線形結合の係数の中にはゼロ以外の係数があります。 したがって、行列の列は線形に依存します。
定理6 もし 行列の列 線形依存している、それだけです
行列の列は線形に依存します。 
証拠。 明確にするために、行列の最初の列は次のように仮定します。
直線的に依存します。 次に、線形依存の定義により、少なくとも 1 つが非ゼロである一連の数値が存在し、これらの係数を持つ列の線形結合はゼロに等しくなります。
係数がゼロの残りの列を含む、行列のすべての列の線形結合を作成しましょう。
しかし 。 したがって、行列のすべての列は線形に依存します。結果
。 線形独立行列列の中では、いずれも線形独立しています。 (この命題は矛盾によって簡単に証明できます。)
定理7
行列の列が線形従属であるためには、行列の少なくとも 1 つの列が他の列の線形結合であることが必要かつ十分です。
証拠。必要性。
明確にするために、 と仮定しましょう。 つまり、最初の列は残りの列の線形結合になります。
適切性。 行列の少なくとも 1 つの列が他の列の線形結合であるとします。たとえば、 です。ここで、 はいくつかの数字です。
つまり、列の線形結合は 0 に等しく、線形結合内の数値のうち、少なくとも 1 つ ( で ) は 0 とは異なります。
行列のランクを とします。 次数 1 のゼロ以外のマイナーが呼び出されます。 基本的な 。 交点に基底マイナーがある行と列は、と呼ばれます。 基本的な .
線形代数
スラウ理論
行列、行列を使った演算、逆行列。 行列方程式とその解。
マトリックス– 任意の数値を特定の順序で並べた長方形のテーブル。サイズは m*n (行×列) です。 行列の要素は、i が行番号、aj が列番号として指定されます。
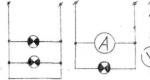
追加 （引き算)行列は 1 次元行列に対してのみ定義されます。 行列の和（差）は、要素がそれぞれ元の行列の要素の和（差）である行列です。
乗算（除算）数字ごとに– この数値による各行列要素の乗算 (除算)。
行列の乗算は、最初の列の数が 2 番目の行の数と等しい行列に対してのみ定義されます。
行列乗算– 行列。その要素は次の式で与えられます。
行列転置– このような行列 B の行 (列) は元の行列 A の列 (行) です。 指定された
逆行列
行列方程式– A*X=B の形式の方程式は行列の積であり、この方程式の答えは行列 X であり、次の規則を使用して求められます。
行列の列 (行) の線形依存性と独立性。 線形依存基準、行列の列 (行) の線形依存の十分条件。
行 (列) のシステムはと呼ばれます。 線形独立、線形結合が自明である場合 (等式は a1...n=0 についてのみ成り立ちます)、ここで A1...n は列 (行)、aa1...n は展開係数です。
基準: ベクトル系が線形依存するためには、系のベクトルの少なくとも 1 つが系の残りのベクトルを通じて線形に表現されることが必要かつ十分です。
十分な条件:
行列行列式とその性質
行列行列式 (行列式)– 正方行列 A の場合、次の式を使用して行列の要素から計算できる数値。
、ここで、要素の追加のマイナーは
プロパティ:
逆行列、逆行列を計算するアルゴリズム。
逆行列– このような正方行列 X は、同じ次数の正方行列 A とともに次の条件を満たします。ここで、E は A と同じ次数の単位行列です。 行列式が 0 に等しくない正方行列は 1 になります。 逆行列。 基本変換の方法と次の式を使用して求められます。
マトリックスランクの概念。 マイナー基底定理。 行列の行列式がゼロに等しいかどうかの基準。
行列の初等変換。初等変換の方法を使用したランク計算。 初等変換の方法を使用した逆行列の計算。
マトリックスランク –基底マイナー次数 (rg A)
基本マイナー –次数 r のマイナーが 0 に等しくありません。つまり、次数 r+1 以上のすべてのマイナーが 0 に等しいか、存在しません。
基本マイナー定理 -任意の行列 A の各列 (行) は、基底マイナーが位置する列 (行) の線形結合です。 証拠：次元 m*n の行列 A の基底マイナーが最初の r 行と最初の r 列に位置するとします。 対応する要素を行列 A の基底マイナーに割り当てることによって得られる行列式を考えてみましょう。
s 行目 
そしてk番目の列。 
任意の u について、この行列式はゼロに等しいことに注意してください。 or の場合、行列式 D には 2 つの同一の行または 2 つの同一の列が含まれます。 そうである場合、行列式 D は (r+λ)-ro 次数のマイナーであるため、ゼロに等しくなります。 最後の行に沿って行列式を展開すると、次が得られます。 ここで、 は最後の行の要素の代数補数です。 基本マイナーなので注意。 したがって、どこで 最後の等式を書くと、次のようになります。、つまり
k番目の列(どのような場合でも) 基底短音の列の線形結合があり、これを証明する必要がありました。基準 d
etA=0:
– 行列式は、その行 (列) が線形従属している場合に限り、ゼロに等しくなります。
基本的な変換
1) 文字列にゼロ以外の数値を乗算する。
2) ある行の要素に別の行の要素を追加します。
3) 文字列の再配置。
4) 同一の行 (列) の 1 つを取り消し線で消します。 5）転置。
逆行列の計算- 変換は、特定の行列 T に、対応する基本行列の積である行列 A を乗算することによって実装できます: TA = E。
この式は、変換行列 T が行列 の逆行列であることを意味します。 したがって、
サイズが mxn の、必ずしも正方形ではない任意の行列 A を考えてみましょう。
マトリックスのランク。
行列のランクの概念は、行列の行 (列) の線形依存 (独立) の概念に関連付けられています。 この概念を文字列について考えてみましょう。 列の場合も同様です。
行列 A のドレインを表します。
e 1 =(a 11,a 12,…,a 1n); e 2 =(a 21,a 22,…,a 2n);…, e m =(a m1,a m2,…,a mn)
a kj =a sj 、j=1,2,…,n の場合、 e k =es
行列の行に対する算術演算 (加算、数値による乗算) は、要素ごとに実行される演算として導入されます。
e k +е s =[(a k1 +a s1),(a k2 +a s2),…,(a kn +a sn)]。
行eが呼び出されます 線形結合行 e 1、e 2、…、ek、これらの行と任意の実数の積の合計に等しい場合:
e=λ 1 e 1 +λ 2 e 2 +…+λ k e k
行 e 1、e 2、…、em は呼び出されます。 、線形結合のすべての係数がゼロに等しい場合にのみ、それらの線形結合がゼロに等しい場合。 行列の列は次のように呼ばれます。、すべてがゼロに等しいわけではない実数 λ 1 ,λ 2 ,…,λ m がある場合、これらの文字列の線形結合はゼロ文字列と等しくなります: λ 1 e 1 +λ 2 e 2 +…+λ m e m = 0 、どこ 0 =(0,0,…,0) (1)
すべての係数 λ i がゼロに等しい場合 (λ 1 =λ 2 =...=λ m =0)、線形結合がゼロに等しい場合、行 e 1、e 2、...、私たちは呼ばれています 線形的に独立しています。
定理1。 文字列 e 1 、e 2 、…、e m が線形従属であるためには、これらの文字列の 1 つが残りの文字列の線形結合であることが必要かつ十分です。
証拠. 必要性。 文字列 e 1、e 2、…、em が線形従属であるとします。 念のため言っておきますが、 (1) λ m ≠0 の場合
それ。 文字列 e m は、残りの文字列の線形結合です。 等。
適切性。 文字列の 1 つ (e m など) を残りの文字列の線形結合とします。 次に、等式が成り立つような数値があり、これは次の形式で書き換えることができます。
ここで、係数の少なくとも 1 つ (-1) はゼロに等しくありません。 それらの。 行は線形依存しています。 等。
意味。 マイナー k 次オーダーサイズ mxn の行列 A は、行列 A の任意の k 行と任意の k 列の交点にある要素を持つ k 次行列式と呼ばれます (k≤min(m,n))。 。
例。、第 1 順位未成年者: =、=;
2次未成年者: 、3次
3 次行列には 9 つの 1 次マイナー、9 つの 2 次マイナー、および 1 つの 3 次マイナー (この行列の行列式) があります。
意味。 行列 A のランクは、この行列のゼロ以外のマイナーの最高次数です。 指定 - rg A または r(A)。
行列のランクのプロパティ.
1) 行列 A nxm のランクは、その次元の小さい方を超えません。つまり、
r(A)≤min(m,n)。
2) すべての行列要素が 0 に等しい場合、r(A)=0。つまり、 A=0。
3) n 次の正方行列 A の場合、r(A)=n、A が非縮退の場合。
(ランク 対角行列非ゼロの対角要素の数に等しい)。
4) 行列のランクが r に等しい場合、行列には 0 に等しくない次数 r のマイナーが少なくとも 1 つあり、より高い次数のマイナーはすべて 0 に等しくなります。
マトリックスのランクには次の関係が当てはまります。
2) r(A+B)≤r(A)+r(B)。 3) r(AB)≤min(r(A),r(B));
3) r(A+B)≧|r(A)-r(B)|; 4) r(A T A)=r(A);
5) r(AB)=r(A)、B が正方非特異行列の場合。
6) r(AB)≥r(A)+r(B)-n、n は行列 A の列数または行列 B の行数です。
意味。次数 r(A) のゼロ以外のマイナーが呼び出されます 基本マイナー。 (行列 A には複数の基底マイナーが含まれる場合があります)。 基底マイナーがある交点にある行と列をそれぞれ呼びます。 基本文字列そして ベースカラム.
定理 2 (基底マイナーについて)。基礎となる行 (列) は線形に独立しています。 行列 A の任意の行 (任意の列) は、基底行 (列) の線形結合です。
証拠。 (文字列の場合)。 基本行が線形従属である場合、定理 (1) によれば、これらの行の 1 つは他の基本行の線形結合となり、基本マイナーの値を変更せずに、指定された線形結合をこの行から減算できます。これは、基底マイナーがゼロとは異なるという事実と矛盾します。 それ。 基底行は線形独立です。
行列 A の任意の行が基底行の線形結合であることを証明しましょう。 なぜなら 行 (列) を任意に変更しても、行列式はゼロに等しいという性質を保持します。その場合、一般性を失うことなく、マイナー基底が行列の左上隅にあると仮定できます。
あ=、それらの。 最初の r 行、最初の r 列にあります。 1ポンドjポンド、1ポンドiポンドとしましょう。 (r+1) 次の行列式が成り立つことを示しましょう。
j£r または i£r の場合、この行列式はゼロに等しくなります。 2 つの同一の列または 2 つの同一の行が含まれます。
j>r かつ i>r の場合、この行列式は行列 A の (r+1) 次のマイナーになります。 行列のランクは r に等しく、これは、より高い次数のマイナーは 0 に等しいことを意味します。
最後の (追加された) 列の要素に従って展開すると、次のようになります。
a 1j A 1j +a 2j A 2j +…+a rj A rj +a ij A ij =0、ここで最後の代数補数 A ij は基底マイナー M r と一致するため、A ij = M r ≠0。
最後の等式を A ij で割ると、要素 a ij を線形結合として表すことができます。
i の値 (i>r) を固定し、任意の j (j=1,2,…,n) について要素が i 行目 e i は、直線 e 1、e 2、…、er r の要素を通じて線形に表現されます。 i 行目は、基本文字列の線形結合です: 。 等。
定理 3. (行列式がゼロに等しいための必要十分条件)。 n 次の行列式 D がゼロになるためには、その行 (列) が線形従属であることが必要かつ十分です。
証明（p.40）. 必要性。 n 次の行列式 D がゼロに等しい場合、その行列の基底マイナーは次数 r になります。 したがって、1 つの行は他の行の線形結合になります。 次に、定理 1 により、行列式の行は線形従属になります。 適切性。 行 D が線形従属である場合、定理 1 により、1 つの行 A i は残りの行の線形結合になります。 D の値を変更せずに、指定された線形結合を文字列 A i から減算すると、ゼロの文字列が得られます。 したがって、行列式の性質によれば、D=0 となります。 等 定理4.基本的な変換中、行列のランクは変化しません。 証拠。 行列式の性質を考えるときに示したように、正方行列を変換すると、行列式は変化しないか、ゼロ以外の数値が乗算されるか、符号が変わります。 この場合、元の行列の非ゼロのマイナーの最高次数が保存されます。 マトリックスのランクは変わりません。 等。 r(A)=r(B) の場合、A と B は次のようになります。 相当：A～B。 定理5.基本的な変換を使用すると、行列を次のように縮小できます。 階段状の眺め。マトリックスはと呼ばれます 段階的に、次の形式の場合: A=、a ii ≠0、i=1,2,…,r; r≦k。 r≤k という条件は、転置によって常に達成できます。 定理6.エシュロン行列のランクは、その非ゼロ行の数に等しい .
それらの。 ステップ行列のランクは r に等しいため、 次数 r の非ゼロのマイナーがあります: 行列行の線形独立性
サイズ行列が与えられた場合 行列の行を次のように表します。 2 つの行は次のように呼ばれます。 等しい
、対応する要素が等しい場合。 。 要素ごとに実行される演算として、文字列に数値を乗算し、文字列を加算する演算を紹介します。 意味。行が、これらの行と任意の実数 (任意の数値) との積の合計に等しい場合、その行は行列行の線形結合と呼ばれます。 意味。行列の行は次のように呼ばれます。 、線形結合のすべての係数がゼロに等しい場合にのみ、それらの線形結合がゼロに等しい場合。 行列の列は次のように呼ばれます。
、行列行の線形結合がゼロ行と等しくなるように、同時にゼロに等しくない数値がある場合: どこ 。 (1.1) 行列の行の線形依存性とは、行列の少なくとも 1 行が残りの行の線形結合であることを意味します。 意味。すべての係数が である場合に限り、行の線形結合 (1.1) がゼロに等しい場合、その行は呼び出されます。 行列の列は次のように呼ばれます。
. 行列の順位定理.
行列のランクは、他のすべての行 (列) が線形的に表現される、線形的に独立した行または列の最大数に等しくなります。 この定理は行列解析、特に連立一次方程式の研究において基本的な役割を果たします。 6、13、14、15、16。 ベクトル。 ベクトルの演算 (加算、減算、数値による乗算)、n
-次元ベクトル。 ベクトル空間の概念とその基礎。
ベクトルは、2 つの大文字、または 1 つの小文字と線または矢印のいずれかで指定できます。 長さ（またはモジュール）
ベクトルは、ベクトルを表す線分 AB の長さに等しい数値です。 同じ線上または平行線上にあるベクトルを と呼びます。 同一直線上にある
. ベクトルの始まりと終わりが一致する場合 ()、そのようなベクトルは と呼ばれます。 ゼロ
= で表されます。 ゼロベクトルの長さはゼロです。 1) ベクトルと数値の積:
の場合はベクトルの方向と一致し、 の場合はその逆の長さのベクトルが存在します。 2) 反対のベクトル
- ベクトルと数値 (-1) の積と呼ばれます。つまり、 -=。 3) 2 つのベクトルの合計
そしてベクトルが呼び出されます。その開始はベクトルの開始と一致し、終了はベクトルの終了と一致します (開始が終了と一致する場合)。 （三角形の法則）。 いくつかのベクトルの合計も同様に求められます。 4) 2つのベクトルの差
そして は、ベクトルとベクトル - の和、反対と呼ばれます。 内積
意味: 2 つのベクトルのスカラー積は、これらのベクトルの長さとそれらの間の角度の余弦の積に等しい数値です。 n次元ベクトルとベクトル空間
意味。 n 次元ベクトルは順序付けられたコレクションです n
フォームに書かれた実数 x = (x 1,x 2,…,x n)、 どこ x i
– 私
ベクトルの - 番目の成分 ×. n 次元ベクトルの概念は経済学で広く使用されており、たとえば、特定の商品セットはベクトルによって特徴付けることができます。 x = (x 1,x 2,…,x n),とそれに対応する価格 y = (y 1,y 2,…,y n)。 - 2 つの n 次元ベクトルは等しい
対応するコンポーネントが等しい場合にのみ、つまり、 x=y、xの場合 私= y 私, 私 = 1,2,…,n. - 2 つのベクトルの合計
同じサイズ nベクトルと呼ばれる z = x + y、その成分は被加数ベクトルの対応する成分の合計に等しい、つまり z 私= x 私+y 私、i = 1、2、…、 n. - ベクトル x と実数の積
は、その成分がベクトルの対応する成分の積に等しいベクトルと呼ばれます。 、 私= 1,2,…,n. 任意のベクトルに対する線形演算は、次の特性を満たします。
1) - 和の可換(可換)性質。 2) - 合計の結合（組み合わせ）特性。 3) - 数値因子に関する結合特性。 4） - ベクトルの合計に対する分配（分配）特性。 5) - 数値因子の合計に関する分配特性。 6) あらゆるベクトルに対して次のようなゼロ ベクトルが存在します (ゼロ ベクトルの特別な役割)。 7) 任意のベクトルに対して、次のような反対のベクトルが存在します。 8) 任意のベクトル (数値係数 1 の特別な役割)。 意味。 上記の 8 つの性質 (公理とみなされる) を満たす数値をベクトルに加算したり、ベクトルに乗算したりする演算が定義されている、実数成分を含むベクトルの集合は、と呼ばれます。 ベクトル状態
. 寸法と根拠 ベクトル空間
意味. 線形空間呼ばれた n次元
、存在する場合 n線形独立ベクトルであり、いずれかのベクトルがすでに依存しています。 言い換えると、 空間の次元
は、それに含まれる線形独立ベクトルの最大数です。 数値 n は空間の次元と呼ばれ、 で表されます。 n 次元空間内の n 個の線形独立ベクトルのセットはと呼ばれます。 基礎
. 7. 行列の固有ベクトルと固有値。 行列の特性方程式。
意味。 ベクトルは次のように呼ばれます 固有ベクトル
線形演算子、次のような数値がある場合: その番号を適正といいます 演算子の値
(行列 あ)、ベクトル に対応します。 行列形式で書くことができます。 ここで、 はベクトル座標の列行列、または拡張形式です。 右側にゼロが来るようにシステムを書き直してみましょう。 行列式は多項式です nに対する 番目の度。 この多項式は次のように呼ばれます 演算子の特性多項式
または行列 A の場合、結果として得られる方程式は次のようになります。 演算子の特性方程式
または行列 A。 例：
行列で与えられた線形演算子の固有値と固有ベクトルを求めます。 解決策: 特性方程式を作成します。 固有値に対応する固有ベクトルを見つけます。 これを行うには、行列方程式を解きます。 または または 。 を仮定すると、任意のベクトル が固有値を持つ線形演算子の固有ベクトルであることがわかります。 同様に、ベクトル 。 8. システム nとの一次方程式 n変数 (一般的なビュー)。 そんなシステムをマトリクス形式で記録。 システムソリューション (定義)。 一貫したものと互換性のないもの、明確な一次方程式系と不明確な一次方程式系。
未知数を含む連立一次方程式を解く
連立一次方程式は経済学で広く使用されています。 変数を含む一次方程式系は次の形式になります。 ここで、() は任意の番号です。 変数の係数
そして 方程式の自由項
、 それぞれ。 簡単なエントリ: ()。 意味。システムの解はそのような値のセットであり、これを代入するとシステムの各方程式が真の等式になります。 1) 連立方程式は次のように呼ばれます。 ジョイント
少なくとも 1 つの解決策がある場合、および 非接合解決策がない場合。 2) 連立方程式系は次のように呼ばれます。 ある
独自の解決策がある場合、そして 不確かな
複数の解決策がある場合。 3) 2 つの方程式系が呼び出されます。 同等 (同等)
、同じソリューションのセット (たとえば、1 つのソリューション) がある場合。 システムを行列形式で書いてみましょう。
次のように示しましょう: あ– 変数の係数の行列、またはシステムの行列、 ×
– 変数の行列列、 で
– 無料会員のマトリックス列。 なぜなら 行列の列数が行列の行数と等しい場合、その積は次のようになります。 列マトリックスがあります。 結果として得られる行列の要素は、初期システムの左側の部分です。 行列の等価性の定義に基づいて、初期システムは次の形式で記述できます。 クラマーの定理.
をシステムの行列の行列式とし、 を 番目の列を自由項の列に置き換えることによって行列から得られる行列の行列式とします。 次に、 の場合、システムには次の式によって決定される固有の解決策があります。 クレーマーの公式。 例。 Cramer の公式を使用して連立方程式を解く
解決。 システム行列の決定要因。 したがって、このシステムには独自のソリューションがあります。 1 番目、2 番目、3 番目の列をそれぞれ自由項の列に置き換えて得られる を計算してみましょう。 クレイマーの公式によれば、次のようになります。 9. システムを解くためのガウス法n
との一次方程式 n変数。 ジョルダン・ガウス法の概念。
ガウス法
- 変数を順次削除する方法。 ガウス法は、基本的な行変換と列の置換を使用して、方程式系をステップ (または三角形) 形式の等価な系に変換し、そこから他のすべての変数を最後の変数 (数値による）変数。 方程式そのものではなく、自由項の列を行列に割り当てることで得られる係数の拡張行列を使用してガウス変換を実行すると便利です。 ガウス法は次の形式の方程式系を解くことができることに注意してください。 例。 ガウス法を使用してシステムを解きます。
システムの拡張行列を書き留めてみましょう. ステップ1
.
1行目と2行目を入れ替えて1にしましょう。 ステップ2。
最初の行の要素に (-2) と (-1) を掛けて、2 行目と 3 行目の要素に加算して、1 列目の要素の下にゼロが表示されるようにしましょう。 。 連立一次方程式系では、次の定理が当てはまります。
定理1.結合システムの行列のランクが変数の数と等しい場合、つまり、 の場合、システムには独自のソリューションがあります。 定理2.結合システムの行列のランクが変数の数より小さい場合、つまり、 の場合、システムは不確実であり、無限の数の解があります。 意味。行列の基底マイナーは、次数が行列のランクと等しい非ゼロのマイナーです。 意味。係数が基本マイナーの表記に含まれる未知数は基本 (または基本) と呼ばれ、残りの未知数は自由 (または非基本) と呼ばれます。 この場合の連立方程式を解くということは、 と (それらの係数で構成される行列式はゼロに等しくないため) を表現することを意味し、 と は自由未知数になります。 基本変数を自由変数で表現してみましょう。 結果の行列の 2 行目から変数を表します。 最初の行から次のように表現します。 連立方程式の一般解: 、 。 行と列 行列として見ることができます 行行列そしてそれに応じて、 列行列。 したがって、他の行列と同様に、それらに対しても次のことを実行できます。 線形演算。 加算演算の制限は、行 (列) が同じ長さ (高さ) でなければならないことですが、この条件は、同じ行列の行 (列) については常に満たされます。 行 (列) の線形演算により、式 α 1 a 1 + ... + α s a s の形式で行 (列) を構成できます。ここで、a 1, ..., a s は任意の行 (列) のセットです。 ) は同じ長さ (高さ) であり、α 1 , ..., α s は実数です。 このような表現はこう呼ばれます 行（列）の線形結合. 定義 12.3. 行(列) 1、...、s が呼び出されます 線形に独立しており、平等なら α 1 a 1 + ... + α s a s = 0、(12.1) ここで、右側の 0 はゼロの行 (列) であり、α 1 = ... = a s = 0 の場合にのみ可能です。それ以外の場合は、ゼロに等しくない実数 α 1 、...、α s がある場合です。同時に、等式 (12.1) が満たされると、これらの行 (列) は と呼ばれます。 、線形結合のすべての係数がゼロに等しい場合にのみ、それらの線形結合がゼロに等しい場合。 行列の列は次のように呼ばれます。. 次のステートメントは線形依存性テストとして知られています。 定理12.3。行 (列) a 1、...、a s、s > 1 は、そのうちの少なくとも 1 つが他の行 (列) の線形結合である場合に限り、線形従属になります。 ◄ 行の証明を実行します。列についても同様です。 必要性。 文字列 a 1 , ..., a s が線形従属である場合、定義 12.3 によれば、同時にゼロに等しくない実数 α 1 , ..., α s が存在します。 a 1 +... + α s a s = 0。ゼロ以外の係数 αα i を選択しましょう。 具体的にはこれをα 1 とする。 次に、α 1 a 1 = (-α 2)a 2 + ... + (-α s)a s となり、したがって、a 1 = (-α 2 /α 1)a 2 + ... + (-α s /α 1)a s 、つまり 文字列 a 1 は、残りの文字列の線形結合として表されます。 適切性。 たとえば、a 1 = λ 2 a 2 + ... + λ s a s とします。 この場合、1a 1 + (-λ 2)a 2 + ... +(-λ s)a s = 0 となります。線形結合の最初の係数は 1 に等しくなります。 それはゼロではありません。 定義 12.3 によれば、文字列 a 1 、...、a s は線形従属です。 定理12.4。行（列） a 1 、...、a s を線形独立とし、行（列） b 1 、...、b l の少なくとも 1 つをそれらの線形結合とする。 この場合、すべての行 (列) a 1、...、a s、b 1、...、b l は線形従属になります。 ◄ たとえば、b 1 が a 1、...、a s の線形結合であるとします。 b 1 = α 1 a 1 + ... + α s a s 、α i ∈R、i = 1,s 。 この線形結合に、係数ゼロの行 (列) b 2、...、b l (l > 1 の場合) を追加します。 b 1 = α 1 a 1 + ... + α s a s + 0b 2 + ... + 0bl。 定理 12.3 によれば、行 (列) a 1 , ..., a s , b 1 , ..., b i は線形従属です。
ベクトルは始点を持つ有向線分です あそして終点 で(それ自体と平行に移動できます)。
または行列形式: 。 結果として得られる均質なシステムは常にゼロ解を持ちます。 非ゼロ解が存在するためには、系の行列式が以下であることが必要かつ十分です。
または 、そこから線形演算子の固有値。
、または 、次の場所から: 、または
,
、 どこ
.
.
