で ベクトル空間 V 任意のフィールド上で P リニアに設定 演算子。

定義9.8。 コア線形演算子  は空間内のベクトルの集合です V、そのイメージはゼロ ベクトルです。 承認されました このセットの表記法: カー、つまり

カー = {× | (×) = ああ}.

定理9.7。線形演算子のカーネルは空間の部分空間です V.

定義9.9。寸法 線形演算子のカーネルは次のように呼ばれます。 欠陥線形演算子。 ディム・カー = d.

定義9.10。ある意味では線形演算子  は画像のセットです 空間ベクトル V。 このセットの表記 私は、つまり 私は = {(×) | × V}.

定理9.8。画像 線形演算子は空間の部分空間です V.

定義9.11。寸法 線形演算子のイメージは次のように呼ばれます。 ランク線形演算子。 薄暗い 私は = r.

定理9.9。空間 Vカーネルとその中で指定された線形演算子のイメージの直接和です。 線形演算子のランクと欠陥の合計は空間の次元に等しい V.

例9.3。 1) 宇宙で R[×] ( 3) ランクと欠陥を見つける オペレーター 差別化。 導関数がゼロに等しい多項式を見つけてみましょう。 これらは 0 次の多項式であるため、 カー = {f | f = c） そして d= 1. 次数が 3 を超えない多項式の導関数は、次数が 2 を超えない多項式のセットを形成します。したがって、次のようになります。 私は =R[×] ( 2) および r = 3.

2) 線形の場合 演算子は行列で与えられます M()、そのカーネルを見つけるには、次のことを解決する必要があります。 方程式( ×) = ○、行列形式では次のようになります。 M()[×] = [○]。 から したがって、線形演算子のカーネルの基礎は、基礎となる行列を持つ同次一次方程式系の基本的な解のセットであるということになります。 M()。 線形演算子のイメージのジェネレータ システム ベクトルを構成します ( e 1), (e 2), …, (e n）。 このベクトル系の基礎は、線形演算子のイメージの基礎を与えます。

9.6. 可逆線形演算子

意味9.12. リニア 演算子が呼び出されます 可逆、存在する場合 リニア オペレーター ψ そのような 何が行われているのか 等式 ψ = ψ = 、ここで  は恒等演算子です。

定理9.10。線形の場合 オペレーター  リバーシブル、 それ オペレーター ψ は一意に定義され、呼ばれます 逆行する のために 演算子。

この場合、演算子、演算子の逆数 、 –1 と表記されます。

定理9.11。線形演算子  は、その行列が可逆である場合にのみ可逆です M()、一方 M( –1) = (M()) –1 .

この定理から、可逆線形演算子の階数は次と等しいことがわかります。 寸法 スペースがあり、欠陥はゼロです。

例9.4 1) 線形が反転可能かどうかを判断する 演算子 , if ( ×) = (2× 1 – × 2 , –4× 1 + 2× 2).

解決。 この線形演算子の行列を作成してみましょう。 M() = 。 なぜなら
= 0 の場合は行列 M() は不可逆、つまり不可逆で線形であることを意味します。 オペレーター .

2) 探す リニア オペレーター、 戻る 演算子  (場合) (×) = (2× 1 + × 2 , 3× 1 + 2× 2).

解決。この線形の行列 に等しい演算子 M() =
| なので、可逆です。 M()| ≠ 0. (M()) –1 =
したがって、 –1 = (2× 1 – × 2 , –3× 1 + 2× 2).

1

離散情報の統合原理の明確化 別々の認識複雑なオブジェクトの要素は、学際的な緊急の問題です。 この記事では、オブジェクトの画像を構築するプロセスについて説明します。オブジェクトは、一連の小さな要素を組み合わせたブロックの複合体です。 紛争状況が研究対象として選ばれたのは、情報を分析するための一定の戦略があり、一貫して注目の分野にあったからです。 状況の状況はオブジェクトの構成要素であり、紛争のプロトタイプとして個別に認識されました。 この研究の課題は、問題のある行動状況のイメージを反映するマトリックスを数学的に表現することでした。 この問題の解決策は、グラフィック構成のデザインの視覚的分析から得られたデータに基づいており、その要素は状況に応じて対応していました。 サイズと グラフィック機能選択された要素とその構成内での分布は、画像マトリックスの行と列を識別するためのガイドとして機能しました。 研究では、マトリックスの設計は、第一に行動の動機によって、第二に、状況要素の因果関係と情報取得の順序によって、そして第三に、ピースの選択によって決定されることが示されました。重み付けパラメータに従って情報を抽出します。 行動状況の画像を形成する上記の行列ベクトル原理は、注意が向けられる画像および他のオブジェクトを構築する際の特徴であると仮定することができる。

視覚化

感知

情報の離散性

1. アノーキン P.K. 生理学に関するエッセイ 機能システム。 – M.: 医学、1985. – 444 p.

2. イリン V. A.、ポズニャク E. G. 線形代数：大学向けの教科書。 – 第 6 版 – M.: フィズマトリット、2004。-280 p。

3. ラヴロフ V.V. 脳と精神。 – サンクトペテルブルク: RGPU、1996. – 156 p.

4. ラヴロフ V.V.、ラヴロワ N.M. 紛争状況のイメージの完全性、完全性、価値観および主観性に対する攻撃性の影響 // 認知心理学：学際的な研究と統合的実践。 – サンクトペテルブルク: VVM、2015. – P. 342-347。

5. ラヴロフ V.V.、ルディンスキー A.V. 不完全なものを認識するときの 3 つの情報処理戦略 ビジュアルイメージ// 基礎研究。 – 2014 – 第 6 号 (2)。 – 375～380ページ。

6. ラヴロフ N.M.、ラヴロフ V.V.、ラヴロフ N.V. 調停：責任ある決定を下すこと。 – M: OPPL、2013. – 224 p.

7. Shelepin Yu.E.、Chikhman V.N.、Foreman N. 断片化された画像の知覚の研究の分析 - 全体的な知覚と有益な特徴に基づく知覚//ロシアの生理学的ジャーナル。 2008. – T. 94. No. 7. – P. 758-776。

不完全な画像の知覚に関する研究の結果は、離散情報の統合と完全な画像のモンタージュを決定する原理を研究する視野を広げました。 変化する数の断片が提示されたときの断片化された画像の認識機能の分析により、情報欠乏の状況で完全な画像を構築するための 3 つの戦略を追跡することが可能になりました。 戦略は、一貫した画像を形成するために利用可能な情報の重要性の評価において異なりました。 言い換えれば、各戦略は、利用可能な情報の重みパラメータの操作によって特徴づけられました。 最初の戦略は、画像の断片の同等性を提供します。その識別は、提示されたオブジェクトを完全に理解するのに十分なレベルまで情報が蓄積された後に実行されます。 2 番目の戦略は、利用可能な情報の重みを評価するための差別化されたアプローチに基づいていました。 評価は、オブジェクトの本質に関して立てられた仮説に従って行われました。 3 番目の戦略は、利用可能な情報を最大限に活用するという動機によって決定され、情報は重要視され、実際のオブジェクトの記号またはプロトタイプと見なされます。 重要な点以前の研究では、支配的な感情と行動の動機に応じて戦略の変更を確実にする脳のメカニズムを調べました。 これは、非特異的な脳システムと、中央制御の制御下で動作する神経モジュールの不均一性を指します。 実施された研究は、文献情報源から知られているものと同様に、完全なイメージにおける情報配信の原理という問題を未解決のままに残した。 質問に答えるには、物体の像の形成を観察する必要がありました。 長い間注意が集中し、イメージを構築するために選択された戦略は変更されません。 紛争状況は、状況を分析するという 2 番目の戦略が常に注目されているため、そのような対象として機能する可能性があります。 紛争当事国は、紛争期間の延長を理由に最初の戦略を拒否し、誤った決定を避けるため、3番目の戦略を適用しなかった。

ターゲットこの研究は、注意が向けられた複雑なオブジェクトのコンポーネントを個別に知覚することによって得られる情報の要素に基づいて画像マトリックスを構築する原理を明らかにすることでした。 我々は、第一に、長時間安定して注意が集中する対象を選択すること、第二に、画像視覚化手法を用いて、対象の知覚中に得られる情報の断片化を追跡すること、そして第三に、マトリックス内の整数分布フラグメントの原理を定式化します。

材料と研究方法

問題のある行動状況は、利用可能な情報を分析するための変更されていない戦略により、安定して注目の領域にある複数のコンポーネントのオブジェクトとして機能しました。 この問題は、家族だけでなく、産業機関や教育機関の従業員間の関係の対立によって引き起こされました。 紛争当事者間の矛盾を解決することを目的とした調停に先立ち、状況のイメージを分析する実験が行われた。 調停交渉が始まる前に、紛争当事者の代表者らは、状況分析を容易にする技術を使った実験に被験者として参加するという申し出を受けた。 視覚化技術には、複雑なオブジェクトのコンポーネントを個別に認識する際に生じるイメージの構築を反映するグラフィック構成の構築が含まれていました。 この技術は、物体の細部に対応する要素のセットから積分画像を形成するプロセスを研究するためのツールとして機能しました。 被験者グループは、28歳から65歳までの女性19名と男性8名で構成されました。 状況の完全な視覚的イメージを得るために、被験者は次のことを行うように依頼されました。 次のステップ： 1）紛争状況の状況、つまり出来事、人々との関係、あなた自身の行動の動機、そしてあなたの周囲の人々を記憶に復元します。 2) 状況の本質を理解するための重要性に応じて状況を評価する。 3) 状況を紛争解決に有利な状況と不利な状況に分けて、それらの関係を追跡してみます。 4) あなたの意見で、状況を特徴づけるそれぞれの状況に適したグラフィック要素 (円、四角、三角形、線、または点) を選択します。 5) グラフィック要素によって伝えられる状況の重要性と関係性を考慮して、グラフィック要素から構成を作成し、得られた構成を紙に描きます。 グラフィック構成が分析され、画像要素の秩序性とサイズ比が評価されました。 ランダムで無秩序な構成は拒否され、被験者は状況の相互関係を再考するように求められました。 一般化された組成分析の結果は、画像マトリックスの数式を定式化するためのガイドとして役立ちました。

研究結果と考察

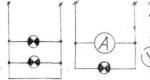
被験者が行動状況のイメージの構築を表現する各グラフィック構成はオリジナルでした。 組成の例を図に示します。

対象者が置かれている問題行動状況の画像を反映したグラフィック構成（構成の各要素は状況状況に対応します）

構成の独自性は、被験者が状況の分析に責任を持って取り組んでいることを証明しています。 特徴的な機能。 構成内の要素の数と要素の寸法、および構成のデザインは、複雑な状況の評価を反映しています。

構図の独創性が注目された後、研究は画像デザインの基本的な特徴を特定することに移りました。 状況のイメージを反映した統合的な構図を構築するために、被験者は状況の因果関係や時間の経過に伴う状況の組み合わせを考慮しながら、個人の好みに従って要素を配分しました。 7 人の被験者は、事前に描かれた比喩的な計画によってその構成が決定された図面の形式で組成物を貼り付けることを好みました。 図では、 図１（ａ、ｂ、ｄ）は、そのような組成物の例を示す。 構成を作成する前に、2 人の被験者は計画の基礎となるアイデアを意識的に選択し、5 人の被験者は選択した選択肢に落ち着いた理由について論理的な説明をせずに直感的に選択しました。 残りの 20 人の被験者は、状況の因果関係と時間の経過に伴う状況の組み合わせのみに注目して、概略的な構図を作成しました (図 1、c、e、f)。 関連した偶然の状況が構成に組み合わされました。 この実験では、グラフィック構成データを使用して紛争の本質を解釈しませんでした。 この解釈はその後、当事者が交渉する準備ができていると判断されたときに、調停の枠組みの中で実行されました。

構図を分析することで、違いだけでなく、状況のイメージを形成する原理の普遍性も追跡することができました。 まず、作品はグラフィック要素で構成されており、それぞれが共通点のある状況を反映しています。 状況の共通性は因果関係と時間的関係によるものでした。 第二に、問題の状況の本質を理解する上で、状況の重要性は等しくありませんでした。 つまり、重みパラメータにおいて事情が異なっていた。 非常に重要な状況が描かれていた グラフィック要素それほど重要でないものと比較してサイズが大きくなります。 画像の注目された特徴は、画像マトリックスをコンパイルするときに考慮されました。 これは、選択された要素のサイズとグラフィックの特徴、およびグラフィック構成におけるそれらの空間的位置が、状況のイメージを反映し、その要素となる情報マトリックスを構築するためのガイドとして機能したことを意味します。 数学的モデル。 テーブルとして表される長方形の行列は、行と列に分割されます。 形成されている問題状況のイメージに関連して、因果関係と時間的関係によって結合されたプロトタイプの重み付けされた要素を含むマトリックスの行と、重みパラメータが異なる要素データを含む列が特定されました。

(1)

個々の線は、イメージの一部、つまりオブジェクトのプロトタイプの形成を反映しています。 線数が多く、m が大きいほど、プロトタイプとして機能した構造的および機能的特性がより完全に考慮されるため、オブジェクトはより完全に認識されます。 列の数 n は、プロトタイプを構築するときに記録された詳細の数によって決まりました。 重みの高い情報と低い情報の断片が蓄積されるほど、プロトタイプは現実とより完全に対応すると考えられます。 マトリックス (1) は、知覚されたオブジェクトのイメージの完成度に応じて次元が変化するため、ダイナミズムを特徴としています。

ここで、完全性が画質の唯一の指標ではないことに注意するのが適切です。 アーティストのキャンバスに表現された画像は、細部や現実との対応の点で写真より劣ることが多いですが、同時に他の画像と組み合わせたり、想像力を刺激したり、感情を刺激したりする点で優れている場合もあります。 この発言は、情報断片の重みを示すパラメータ amn の重要性を理解するのに役立ちます。 体重増加により、入手可能なデータの欠如が相殺されました。 不確実性を克服するための戦略に関する研究が示しているように、入手可能な情報の重要性が高いことを認識すると、問題のある状況での意思決定が促進されます。

したがって、積分画像を形成するプロセスは、それをマトリックス内の情報の操作と関連付けると解釈できます。 操作は、情報断片の重みパラメータの自発的または非自発的（意識的、目的的、または直感的無意識）の変化、つまり amn の値の変化によって表現されます。 この場合、プロトタイプの重要性を特徴付ける値 bm が増加または減少し、同時に結果として得られる画像 br が変化します。 オブジェクトに関する一連のデータをカバーする画像形成のマトリックス モデルに目を向けると、画像の構成は次のように説明されます。 m 個のコンポーネントを含むプリイメージのベクトルを次のように表します。

ここで、T は転置符号であり、プリイメージ ベクトルの各要素は次の形式になります。

次に、結果の画像の選択は、ラプラスの法則に従って実行できます。

ここで、 br は、コンポーネントとして値 bm を持つソリッド イメージの形成の最終結果です。 amn は、プリイメージに対応する行内の変数の位置と重みパラメータを決定する値のセットです。 情報が限られている状況では、利用可能なデータの重みを増やすことで最終結果を増やすことができます。

画像形成の原理に関する提示された資料の議論の最後に、文献には一般的に受け入れられている解釈がないため、「画像」という用語を特定する必要性に注意が向けられます。 この用語は、まず第一に、注目している分野のオブジェクトの詳細に対応する情報断片の統合システムの形成を意味します。 さらに、オブジェクトの大きな詳細は、プロトタイプを構成する情報断片のサブシステムに反映されます。 オブジェクトには、行動状況だけでなく、オブジェクト、現象、プロセスも含まれます。 画像の形成は、受信した情報と、メモリに含まれ、知覚された物体に関連付けられた情報との関連付けによって確実に行われます。 画像を作成する際の情報の断片と関連性の統合は、マトリックスの枠組みの中で実現され、そのデザインとベクトルは意識的または直観的に選択されます。 選択は、行動の動機によって設定された好みによって異なります。 ここでは、基本的な点、つまり積分画像行列を組み立てるために使用される情報の離散性に特別な注意が向けられます。 示されているように、完全性は、受信した情報の分析と記憶への統合のプロセスを制御する非特異的な脳システムによって確保されています。 整合性は、n と m の最小値が 1 に等しい場合に発生します。 画像は利用可能な情報の重みパラメータの増加により高い価値を獲得し、n と m (1) の値が増加するにつれて画像の完全性が増加します。

結論

画像の要素を視覚化することで、問題のある行動の状況を個別に認識する状況で、そのデザインの原則を追跡することが可能になりました。 実行された研究の結果、完全な画像の構築は、マトリックスの構造における情報断片の分布として考えることができることが示されました。 そのデザインとベクトルは、第一に行動動機によって、第二に状況の因果関係と情報取得の時間的順序によって、第三に重みパラメータに従った情報の選択によって決定されます。 画像マトリックスの完全性は、知覚されたオブジェクトを反映する個別の情報を統合することによって保証されます。 非特異的な脳システムは、情報を一貫した画像に統合するメカニズムを構成します。 複雑なオブジェクトの画像形成のマトリックス原理を明確にすると、画像の完全性だけでなく他の特性の性質を理解する視点も広がります。 これは、比喩的なシステムの完全性と安全性、およびその欠如によって生じる価値と主観性を指します。 完全な情報オブジェクトに対して相対的に。

書誌リンク

ラヴロフ V.V.、ルディンスキー A.V. 複雑なオブジェクトの要素を個別に認識する際の統合画像の行列の形成 // 応用および基礎研究の国際ジャーナル。 – 2016. – No. 7-1. – P.91-95;
URL: https://applied-research.ru/ru/article/view?id=9764 (アクセス日: 01/15/2020)。 出版社「自然科学アカデミー」が発行する雑誌をご紹介します。

定義1.線形演算子 A のイメージは、 の形式で表現できるすべての要素のセットです。

線形演算子 A のイメージは、空間の線形部分空間です。 その次元はと呼ばれます オペレーターランク A.

定義2.線形演算子 A のカーネルは、 に対するすべてのベクトルのセットです。

カーネルは空間 X の線形部分空間です。その次元は次のように呼ばれます。 オペレータの欠陥 A.

演算子 A が - 次元空間 X で作用する場合、次の関係 + = が有効です。

オペレーター A が呼び出されます 非退化、そのコアの場合。 非縮退演算子のランクは空間 X の次元に等しい。

ある基底での空間 X の線形変換行列 A であるとすると、画像と逆画像の座標は次の関係によって関連付けられます。

したがって、任意のベクトルの座標は方程式系を満たします。

したがって、線形演算子のカーネルは、特定のシステムの基本的な解のシステムの線形シェルであるということになります。

タスク

1. 演算子のランクが任意の基底での行列のランクと等しいことを証明します。

次の行列によって空間 X の特定の基底で定義された線形演算子のカーネルを計算します。

5. を証明してください。

次の行列で与えられる演算子のランクと欠陥を計算します。

6. . 7. . 8. .

3. 線形演算子の固有ベクトルと固有値

考えてみましょう 線形演算子 A、 - 次元空間 X で動作します。

意味。数値 l は、演算子 A if の固有値と呼ばれます。 この場合、ベクトルは演算子 A の固有ベクトルと呼ばれます。

最も重要な財産線形演算子の固有ベクトルは、ペアごとに異なる固有値に対応する固有ベクトルです。 線形的に独立しています。

が空間 X の基底における線形演算子 A の行列である場合、演算子 A の固有値 l と固有ベクトルは次のように決定されます。

1. 固有値は特性方程式 (次次の代数方程式) の根として求められます。

2. 個々の固有値に対応するすべての線形に独立した固有ベクトルの座標は、一次一次方程式系を解くことによって取得されます。

その行列のランクは です。 このシステムの基本的な解は、固有ベクトルの座標の列ベクトルです。

特性方程式の根は行列の固有値とも呼ばれ、系の解は行列の固有ベクトルと呼ばれます。

例。行列によって特定の基底で指定された演算子 A の固有ベクトルと固有値を求めます

1. 固有値を決定するには、次の特性方程式を作成して解きます。

したがって、固有値、その多重度になります。

2. 固有ベクトルを決定するには、連立方程式を作成して解きます。

基本方程式の等価系は次の形式になります。

したがって、すべての固有ベクトルは列ベクトルであり、c は任意の定数です。

3.1.単純な構造の演算子。

意味。 n 次元空間で動作する線形演算子 A は、正確に n 個の線形独立固有ベクトルに対応する場合、単純構造の演算子と呼ばれます。 この場合、演算子の固有ベクトルから空間基底を構築することが可能です。演算子行列は最も単純な対角形式になります。

ここで、 は演算子の固有値です。 明らかに、その逆も当てはまります。空間 X のある基底で演算子の行列が対角形式を持つ場合、その基底は演算子の固有ベクトルで構成されます。

線形演算子 A は、多重度の各固有値が線形に独立した固有ベクトルに正確に対応する場合に限り、単純な構造の演算子です。 固有ベクトルは連立方程式の解であるため、多重度の特性方程式の各根はランク行列に対応する必要があります。

単純な構造演算子に対応するサイズの行列は、対角行列に似ています。

ここで、元の基底から固有ベクトルの基底への遷移行列 T は、行列の固有ベクトルの座標からの列ベクトルを列として持ちます (演算子 A)。

例。線形演算子行列を対角形式に縮小します

特性方程式を作成し、その根を見つけてみましょう。

多重度と多重度の固有値はどこから来るのでしょうか?

最初の固有値。 これは、座標が次のような固有ベクトルに対応します。

システムソリューション

このシステムのランクは 3 であるため、独立した解は 1 つだけ (たとえば、ベクトル ) だけです。

に対応する固有ベクトルは連立方程式によって決定されます。

ランクは 1 なので、たとえば、線形に独立した解が 3 つあります。

したがって、多重度の各固有値は正確に線形に独立した固有ベクトルに対応するため、演算子は単純な構造の演算子になります。 遷移行列 T の形式は次のとおりです。

同様の行列間の接続は次の関係によって決まります。

タスク

固有ベクトルと固有値を求める

行列によって特定の基底で定義された線形演算子:

次の線形演算子のうち、新しい基底に渡すことで対角形式に変換できるものを決定します。 この基底とそれに対応する行列を求めます。

10. 異なる固有値に対応する線形演算子の固有ベクトルが線形独立であることを証明します。

11. 作用する線形演算子 A が n 個の異なる値を持つ場合、A と交換する線形演算子 B には固有ベクトルの基底があり、A の固有ベクトルは B の固有ベクトルにもなることを証明します。

不変部分空間

定義1.. 亜空間L 線形空間各ベクトルの画像も に属する場合、X は X に作用する演算子 A の下で不変であると言われます。

不変部分空間の主なプロパティは、次の関係によって決まります。

1. と が演算子 A に関して不変部分空間である場合、それらの和と交差も演算子 A に関して不変です。

2. 空間 X が部分空間と () の直接和に分解され、A に関して不変である場合、基底の演算子の行列 (基底の和集合) はブロック行列になります。

ここで、 は正方行列、0 はゼロ行列です。

3. 演算子 A に関する部分空間不変式では、演算子は少なくとも 1 つの固有ベクトルを持ちます。

例1. X で動作する何らかの演算子 A のカーネルを考えてみましょう。定義によります。 させて 。 すると、ゼロベクトルはすべての線形部分空間に含まれるため、 になります。 したがって、カーネルは A の下で部分空間不変量となります。

例2。空間 X の何らかの基底で、演算子 A が次の方程式で定義された行列で与えられるとします。

5. 非縮退演算子 A の下で不変である部分空間は、逆演算子の下でも不変であることを証明します。

6. しましょう 線形変換基底の 1 次元空間には、 対角行列対角線上にさまざまな要素を配置します。 A の下で不変な部分空間をすべて見つけて、その数を決定します。