インパルス応答を知ってフィルターの周波数応答を取得する方法。
テクニカルプレビュー
ノヴォシビルスク州立工科大学
オートメーションおよびコンピュータ工学部
データ収集および処理システム部門
専門分野「理論と信号処理」10
研究室の作業番号
デジタルフィルター
有限インパルス特性付きグループ:
AT-33 1 オプション::
教師学生:
シャドリーナ A.V. 准教授 シチェティニン Yu.I. 仕事の目的:
平滑化窓関数を使用した有限インパルス応答フィルターの解析および合成方法の研究。
1. 仕事を終わらせる:
フィルター長 と の値に対する長方形のウィンドウ カットオフ周波数を持つローパス FIR フィルターのインパルス応答プロット。
 .
.
理想的な離散 FIR フィルターのインパルス応答は無限の長さを持ち、次の負の値では非ゼロになります。
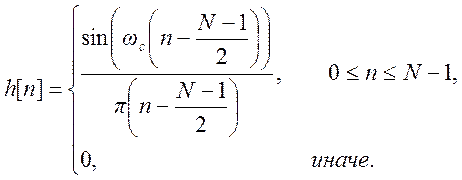
物理的に実現可能なフィルターを取得するには、インパルス応答を有限数に制限し、切り捨てられた応答をある量だけ右にシフトする必要があります。 ![]() 値はフィルターの長さ (サイズ) であり、
値はフィルターの長さ (サイズ) であり、
– フィルタの順序。
Matlab スクリプト (labrab101.m)
N = input("フィルターの長さを入力してください N = ");
h = sin(wc.*(n-(N-1)/2))./(pi.*(n-(N-1)/2);
xlabel("参照番号, n")
>> サブプロット(2,1,1)
>> labrab101
フィルタの長さを入力してください N = 15
>> title("N=15 の FIR フィルターのインパルス応答")
>> サブプロット(2,1,1)
>> サブプロット(2,1,2)
フィルタの長さを入力してください N = 50

>> title("N=50 の FIR フィルターのインパルス応答")
図1。 フィルター長とフィルター長の値に対する長方形のウィンドウ カットオフ周波数を持つローパス FIR フィルターのインパルス応答プロットコメント:  デジタル フィルターの周波数応答をフーリエ級数として考えると、次のようになります。 の場合、この系列の係数はフィルターのインパルス応答の値を表します。 でフーリエ級数は、最初のケースでは に、2 番目のケースでは に切り捨てられ、その後、切り捨てられた特性が参照軸に沿って右にシフトされて、因果フィルターが得られます。 メインローブの幅が 2 の場合と - 1 の場合、つまり フィルターの長さが増加すると、インパルス応答のメインローブが狭くなります。 サイドローブのレベルを ( を使用して) 考慮すると、増加に伴い、絶対値は から まで増加します。 したがって、長方形のウィンドウを備えたフィルターの理想的な周波数応答の近似を使用する場合、メインローブを狭くすること (それによって遷移領域を減らすこと) とサイドローブのレベルを下げること (これを減らすこと) を同時に行うことは不可能であると結論付けることができます。フィルタの通過帯域と阻止帯域のリップル)。 唯一の人 制御パラメータ長方形のウィンドウはそのサイズであり、メインの花びらの幅に影響を与えることができますが、サイドの花びらにはあまり影響を与えません。
デジタル フィルターの周波数応答をフーリエ級数として考えると、次のようになります。 の場合、この系列の係数はフィルターのインパルス応答の値を表します。 でフーリエ級数は、最初のケースでは に、2 番目のケースでは に切り捨てられ、その後、切り捨てられた特性が参照軸に沿って右にシフトされて、因果フィルターが得られます。 メインローブの幅が 2 の場合と - 1 の場合、つまり フィルターの長さが増加すると、インパルス応答のメインローブが狭くなります。 サイドローブのレベルを ( を使用して) 考慮すると、増加に伴い、絶対値は から まで増加します。 したがって、長方形のウィンドウを備えたフィルターの理想的な周波数応答の近似を使用する場合、メインローブを狭くすること (それによって遷移領域を減らすこと) とサイドローブのレベルを下げること (これを減らすこと) を同時に行うことは不可能であると結論付けることができます。フィルタの通過帯域と阻止帯域のリップル)。 唯一の人 制御パラメータ長方形のウィンドウはそのサイズであり、メインの花びらの幅に影響を与えることができますが、サイドの花びらにはあまり影響を与えません。
2. 関数を使用してステップ 1 のインパルス特性の DVFT を計算します。 線形スケールおよびデシベル単位での周波数応答のグラフ 512 周波数サンプル。 フィルターの通過帯域、遷移帯域、阻止帯域。 遷移帯域の幅と通過帯域および阻止帯域の周波数応答リップルのレベルに対するフィルター次数の影響。
MATLAB 関数 (DTFT.m)
関数 = DTFT(x,M)
N = 最大(M, 長さ(x));
% FFT をサイズ 2^m に縮小
N = 2^(ceil(log(N)/log(2)));
% fft を計算する
% 周波数ベクトル
w = 2*pi*((0:(N-1))/N);
w = w - 2*pi*(w>=pi);
% FFT を -pi から +pi の範囲にシフトします
X = fftshift(X);
w = fftshift(w);
Matlab スクリプト (labrab102.m)
h1 = sin(wc.*(n1-(N1-1)/2))./(pi.*(n1-(N1-1)/2);
h2 = sin(wc.*(n2-(N2-1)/2))./(pi.*(n2-(N2-1)/2);
DTFT(h1,512);
DTFT(h2,512);
プロット(w./(2*pi),abs(H1)./max(abs(H1)),,"r")
xlabel("f, Hz")、ylabel("|H1|/max(|H1|)")、グリッド
プロット(w./(2*pi),abs(H2)./max(abs(H2)),"b")
xlabel("f, Hz")、ylabel("|H2|/max(|H2|)")、グリッド
プロット(w./(2*pi),20*log10(abs(H1)),,"r")
title("N = 15 の長方形ウィンドウを持つローパス FIR フィルターの周波数応答")
xlabel("f, Hz")、ylabel("20lg(|H1|), dB")、グリッド
プロット(w./(2*pi),20*log10(abs(H2)),"b")
title("N = 50 の長方形ウィンドウを持つローパス FIR フィルターの周波数応答")
xlabel("f, Hz")、ylabel("20lg(|H2|), dB")、グリッド

図2. フィルター長値に対する長方形のウィンドウカットオフ周波数を備えたローパスFIRフィルターの周波数応答プロットと線形スケール

図3. フィルター長の値に対する長方形のウィンドウカットオフ周波数を備えたローパスFIRフィルターの周波数応答プロットと対数スケール
図1。 フィルター長とフィルター長の値に対する長方形のウィンドウ カットオフ周波数を持つローパス FIR フィルターのインパルス応答プロット
表1. フィルタ長の通過帯域、遷移領域、阻止帯域の範囲と
|
フィルター長 |
帯域幅、Hz |
遷移領域、Hz |
阻止帯域、Hz |
||
48 デジタルフィルター有限インパルス応答を使用します。 KIH フィルターの計算。有限インパルス応答フィルター (非再帰フィルタ, FIRフィルター) または FIR フィルター (FIR は有限インパルス応答 - 有限インパルス応答の略です) - 線形デジタル フィルターの種類の 1 つで、その特徴はインパルス応答の時間制限です (ある時点から、インパルス応答は次の値と正確に等しくなります)。ゼロ)。 このようなフィルターは、フィードバックがないため、非再帰的とも呼ばれます。 このようなフィルターの伝達関数の分母は特定の定数です。 フィルターの入力信号と出力信号の間の関係を表す差分方程式: ここで、 P- フィルタの順序、 ×(n) - 入力信号、 y(n) は出力信号であり、 b 私- フィルター係数。 言い換えれば、出力信号サンプルの値は、スケーリングされた値の合計によって決まります。 P以前の読書。 別の言い方もできます。フィルター出力の値はいつでも、入力の瞬時値に対する応答の値と、徐々に減衰するすべての応答の合計です。 Pまだ出力に影響を与えている前の信号サンプル(後) P-counts では、すでに述べたように、パルス遷移関数はゼロに等しくなります。したがって、その後のすべての項は P-th もゼロになります)。 前の式をより容量の大きい形式で書いてみましょう。
配置したフィルターカーネルを見つけるには ×(n) = δ( n) ここで、δ( n) - デルタ関数。 この場合、FIR フィルターのインパルス応答は次のように記述できます。
インパルス応答の Z 変換により、FIR フィルターの伝達関数が得られます。
]プロパティ FIR フィルターには、IIR フィルターよりも使用する方が望ましい場合がある多くの便利な特性があります。 その一部を次に示します。 FIR フィルターは堅牢です。 FIR フィルターは実装時にフィードバックを必要としません。 FIRフィルターの位相を線形にすることができます FIRフィルターの直接形式 FIR フィルターは、乗算器、加算器、遅延ブロックの 3 つの要素を使用して実装できます。 図に示されているオプションは、タイプ 1 FIR フィルターの直接実装です。
FIR フィルターの直接形式の実装 サンプルプログラム 以下は、C で書かれた FIR フィルター プログラムの例です。 /* 128 タップの FIR フィルター */ float fir_filter(float 入力) 静的フロートサンプル。 acc = 0.0f; /* バッテリー */ /* 乗算と累積 */ for (i = 0; i< 128; i++) { acc += (h[i] * サンプル[i]); /* 出口 */ /* 遅延信号をシフトします */ for (i = 127; i > 0; i--) サンプル[i] = サンプル; 49 データの平滑化。 移動平均。50 データの平滑化。 放物線状の平滑化。51 データの平滑化。 スペンサーのスムージング。52 データの平滑化。 メディアンフィルタリング。移動平均、放物線平滑法、スペンサー平滑法、メディアンフィルタリング 時間の経過とともにゆっくりと変化する物理プロセスのパラメータを決定する方法を開発する場合、重要な課題は、一次コンバータの出力で受信した処理信号に重畳されるノイズ効果やランダムな干渉の影響を排除することです。 この影響を排除するには、データ スムージングを適用します。 このような平滑化の最も簡単な方法の 1 つは、算術平均です。 これを使用すると、離散関数 (処理されたデータ配列) の各値が次の式に従って計算されます。 ここで、 は算術平均のポイント数です (奇数の整数)。 処理前の関数の値。 他にも非常に効果的な平滑化方法があります。たとえば、次の式に従って 5、7、9、11 点の 2 次放物線を使用します。 または、7、9、11、13 点の 4 次の放物線: 実際のアプリケーションでは、15 ポイント スペンサー スムージングなどの他の効果的な方法でも良好な結果が得られます。 これらの式に複素指数関数を代入することで、対応する変換の伝達関数を決定できます。 算術平均の場合 括弧内の式は分母を伴う等比数列を表すため、この式は次のように表すことができます。
この式はローパス フィルターの伝達特性を表しており、平均化に関与する項が多いほど、信号内の高周波ノイズ成分の抑制が大きくなることを示しています (図 6.1 を参照)。 ただし、時間トレンドを処理する場合の周波数の意味概念は、信号を処理する場合の同様の概念とは異なります。 これは、時間の傾向を研究するときに、関心があるのは周波数の構成ではなく、変化の種類 (増加、減少、恒常性、周期性など) であるという事実によって説明されます。 いわゆるヒューリスティック アルゴリズムの使用も、データを平滑化するのに非常に効果的です。 その 1 つはメディアン フィルタリングです。 整数が奇数である次元のスライディング タイム ウィンドウでの実装中に、中央の要素は、平滑化されたデータ配列の要素を値の昇順に並べたシーケンスの中央の要素に置き換えられます。信号が時間枠内に収まります。 メディアン フィルタリングの利点は、滑らかに変化する信号の歪みを実質的に発生させずに、持続時間が超えないインパルス ノイズを除去できることです。 このノイズ抑制方法には厳密な数学的根拠はありませんが、計算の単純さと得られた結果の有効性により、広く使用されています。
図 6.1 - 伝達特性グラフ m=5、7、9、11 の算術平均演算 もう 1 つの興味深い平滑化アルゴリズムは中央値平均です。 その本質は次のとおりです。 サイズ (-奇数整数) のスライディング タイム ウィンドウでは、データ配列の要素が昇順に並べられ、最初と最後の要素が順序付けられたシーケンスから削除されます (<). Центральный элемент временного окна из последовательности сглаживаемых данных заменяется значением, вычисляемым как この方法により、パルスと無線周波数の干渉を抑制し、良好な信号平滑化を実現できます。
すべては、友人の友人の友人が同じフィルターについて助けを必要としたときに始まりました。 ジェダイのやり方で、これに関する噂が私に届き、リンクにある投稿へのコメントで購読を解除しました。 役に立ちそうだった。 そうですね、そう願っています。 この話は、私自身が DSP を受講したときの 3 番目の思い出、またはそのようなものを思い出させ、デジタル フィルターがどのように機能するかに興味はあるが、当然のことながら過度に恐れているすべての人に向けて記事を書こうと思いました。 -トップの数式とサイケデリックな絵(すでに教科書について話しているわけではありません)。 一般に、私の経験では、教科書の状況は、「木を見て森を見ないこともある」という有名なフレーズで説明されています。 つまり、Z 変換や、多くの場合 2 枚のボードよりも長い多項式の除算公式をすぐに怖がらせ始めると、そのトピックへの興味は急速に冷めてしまいます。 幸いなことに、何が起こっているかを理解するために、長く複雑な式を説明する必要はまったくありません。 まず、簡単な基本概念をいくつか説明します。 1. インパルス応答。4 つのピンを備えたボックスがあるとします。 中に何があるのかは分かりませんが、左側の 2 つのターミナルが入口で、右側の 2 つのターミナルが出口であることは確かです。 非常に大きな振幅の非常に短いパルスをそれに加えて、出力で何が起こるかを見てみましょう。 そうですね、この四極子の中に何があるかは明確ではありません。それをどのように説明するかが明確ではないからです。しかし、少なくとも何かが見えるでしょう。 ここで、理論上、大きな(一般的には無限の)振幅を持つ短い(一般的には無限に短い)パルスはデルタ関数と呼ばれると言わなければなりません。 ところで、面白いことに、この積分は 無限の関数は 1 に等しい。 これが正規化です。 したがって、入力にデルタ関数を適用した、四極ネットワークの出力で見られたものは、次のように呼ばれます。 インパルス応答この四極子。 ただし、今のところ、それがどのように役立つかは明らかではありませんが、得られた結果だけを思い出して、次の興味深いコンセプトに移りましょう。 2. 畳み込み。つまり、畳み込みは関数の積を積分する数学的演算です。
ご覧のとおり、アスタリスクで示されています。 また、畳み込み中に 1 つの関数が「前方」の順序で取得され、2 番目の関数が「後ろから前」に処理されることもわかります。 もちろん、人類にとってより価値のある離散の場合、畳み込みは他の積分と同様に合計されます。
それはある種の退屈な数学的抽象化のように思えるでしょう。 しかし、実際には、束はおそらくこの世で最も不思議な現象であり、その素晴らしさでは人の誕生に次ぐものですが、唯一の違いは、ほとんどの人は少なくとも1歳までに子供がどこから来たのかを知ることです。 18 歳のとき、畳み込みとは何か、なぜそれが便利で驚くべきことなのかについては、地球上の人口の大部分が生涯まったく知りません。 したがって、この演算の威力は、f が任意の入力信号、g が 4 ポート ネットワークのインパルス応答である場合、これら 2 つの関数の畳み込みの結果が次のようなものになるという事実にあります。この 4 ポートのネットワークを介して信号 f を通過させることで得られます。 つまり、インパルス応答は、入力エフェクトに関連する 4 ポート ネットワークのすべての特性を完全に反映したものであり、入力信号とそれを畳み込むことで、対応する出力信号を復元できます。 私の意見では、これは本当に素晴らしいことです。3. フィルター。 インパルス応答と畳み込みを使用すると、多くの興味深いことができます。 たとえば、信号がオーディオの場合、リバーブ、エコー、コーラス、フランジャーなどを整理できます。 差別化も統合もできます...一般的には、何でも作成できます。 私たちにとって今最も重要なことは、もちろんフィルターも畳み込みを使用して簡単に取得できるということです。 デジタル フィルター自体は、入力信号と目的のフィルターに対応するインパルス応答の畳み込みです。 ただし、当然のことながら、何らかの方法でインパルス応答を取得する必要があります。 もちろん、上記の測定方法はすでに理解していますが、そのようなタスクではこれにはほとんど意味がありません。フィルターをすでに組み立てている場合、他のものを測定する必要はなく、そのまま使用できます。 さらに、デジタル フィルターの最も重要な価値は、現実には達成できない (または達成が非常に困難な) 特性、たとえば線形位相を持つことができることです。 したがって、ここでは測定する方法はまったくなく、ただカウントする必要があります。4. インパルス応答を取得します。 この時点で、このテーマに関するほとんどの出版物では、著者は大量の Z 変換と多項式からの分数を読者に投げ込み始め、読者を完全に混乱させます。 私はそんなことはしません。これが一体何なのか、そしてなぜ実際には進歩的な大衆にとってそれがあまり必要ではないのかを簡単に説明します。 フィルターに何を求めるかを決定し、それを説明する方程式を作成したとします。 次に、インパルス応答を見つけるには、導出された方程式にデルタ関数を代入して、目的の応答を取得します。 唯一の問題は、これをどのように行うかです。デルタ関数は間に合っているからです。○ ここで彼らはラプラス変換というものがあることを思い出します。 それ自体はレーズン1ポンドではありません。 無線工学でそれが許容される唯一の理由は、まさに、この変換が移行する議論の空間では、いくつかのことが実際に単純になるという事実です。 特に、時間領域で多大な問題を引き起こしたのと同じデルタ関数が非常に簡単に表現されます。それは 1 つだけです。 Z 変換 (別名ローラン変換) は、離散システム用のラプラス変換のバージョンです。 つまり、目的のフィルターを記述する関数にラプラス変換 (または必要に応じて Z 変換) を適用し、その結果のフィルターを代入して逆変換することにより、インパルス応答が得られます。 簡単そうに思えますので、誰でも試してみることができます。 すでに述べたように、ラプラス変換、特に逆変換は厳しいものであるため、危険を冒すつもりはありません。 これは最後の手段として残しておき、探しているものを取得するためのより簡単な方法を探します。 それらはいくつかあります。 まず、もう 1 つの驚くべき自然事実を思い出してください。振幅周波数とインパルス特性は、よく知られた優れたフーリエ変換によって相互に関連付けられています。 これは、好みに合わせて任意の周波数応答を描画し、そこから逆フーリエ変換を実行し (連続または離散)、それを実装するシステムのインパルス応答を取得できることを意味します。 これは本当に素晴らしいことです! ただし、これには問題がないわけではありません。 第一に、私たちが得るインパルス応答はおそらく無限になるでしょう (理由については説明しません。それが世界の仕組みです)。そのため、ある時点で自発的にそれを遮断する必要があります (ゼロに設定する)。それを超えて)。 しかし、これはそのままでは起こりません。その結果、ご想像のとおり、計算されたフィルターの周波数応答が歪みます。波状になり、周波数カットオフがぼやけます。
これらの影響を最小限に抑えるために、短縮されたインパルス応答にさまざまな平滑化ウィンドウ関数が適用されます。 その結果、周波数応答は通常さらにぼやけますが、不快な(特に通過帯域での)発振は消えます。 実際、このような処理の後、動作するインパルス応答が得られ、デジタル フィルターを構築できます。 2 番目の計算方法はさらに単純です。最も一般的なフィルターのインパルス応答は、長い間解析形式で表現されてきました。 残っているのは、値を置き換えて、好みに応じて結果にウィンドウ関数を適用することだけです。 したがって、変換を考慮する必要さえありません。 そしてもちろん、目的が特定の回路の動作をエミュレートすることである場合は、シミュレータでそのインパルス応答を取得できます。
ここでは、持続時間 1 μs の 100500 ボルト (はい、100.5 kV) のパルスを RC 回路の入力に印加し、そのインパルス応答を取得しました。 これが実際には実行できないことは明らかですが、シミュレータでは、ご覧のとおり、この方法はうまく機能します。 5. 注意事項。インパルス応答の短縮について上で述べたことは、もちろん、いわゆるものに当てはまります。 有限インパルス応答フィルター (FIR/FIR フィルター)。 直線位相 (インパルス応答を構築するための特定の条件下) など、貴重な特性を多数備えています。これにより、フィルタリング中の信号の歪みがなく、絶対的な安定性が保証されます。 無限インパルス応答フィルター (IIR/IIR フィルター) もあります。 計算の点ではリソースの消費量は少なくなりますが、記載されている利点はなくなりました。 次の記事では、デジタル フィルターの実際的な実装の簡単な例を見ていきたいと思います。 最も単純なデジタル フィルター、つまり定数パラメーターを持つフィルターを考えてみましょう。 デジタル フィルターの入力信号は、一定の間隔で続く一連の数値の形式で供給されます (図 4.1、a)。 次の各信号値がデジタル フィルターで受信されると、出力信号の次の値が計算されます。計算アルゴリズムは非常に多様です。 計算プロセス中に、入力信号の最後の値に加えて、 入力信号と出力信号の前の値: デジタル フィルターの出力信号も、 の間隔に続く数値のシーケンスです。 この間隔はデジタル信号処理装置全体で同じである。
米。 4.1. デジタルフィルターの入力と出力の信号 したがって、単一パルスの形式の単純な信号がデジタル フィルターの入力に適用されるとします (図 4.2、a)。
次に、出力では、一定の間隔で続く数値の離散シーケンスの形式で信号を取得します。 従来のアナログ回路と同様に、この応答信号をフィルターのインパルス応答と呼びます (図 4.2、b)。 アナログ回路のインパルス応答とは異なり、この関数は無次元です。
米。 4.2. デジタルフィルターの単位インパルスとインパルス応答 任意の離散信号をフィルター入力に適用してみましょう (図 2)。 4.1、a)、離散値のセット 最初の要素のアクションでは、乗算されたシーケンスがフィルターの出力で形成されます。アクションでは、シーケンスが乗算され、ある量だけ右にシフトされます。その結果、出力は次のようになります。シーケンス
したがって、出力信号は、入力信号とインパルス応答の離散畳み込みとして定義されます。 この点において、デジタル フィルターは従来の回路と同様であり、出力信号は入力信号とインパルス応答の畳み込みに等しくなります。 式(4.1)はデジタルフィルタリングアルゴリズムである。 フィルタのインパルス応答が有限数の項を含むシーケンスで記述される場合、フィルタは図に示す回路の形式で実装できます。 4.3. ここで、文字は時間に対する信号遅延の要素 (セルごと) を示します。 - 信号に対応する係数を乗算する要素。 図に示す図。 4.3 はデジタル フィルターの電気回路ではありません。 この図はデジタル フィルタリング アルゴリズムをグラフで表現したもので、信号処理中に実行される一連の算術演算を示しています。
米。 4.3. 非再帰型デジタルフィルター回路 抽象的な数値シーケンスの形式で信号を処理するデジタル フィルターの場合、「時間遅延」の概念は完全に正しいわけではありません。 したがって、信号を 1 セル遅延させる要素は、通常、デジタル フィルター回路上で、変換の言語で信号遅延を示す記号でマークされます。 以下では、この表記に従います。 図のデジタルフィルター回路に戻りましょう。 4.3、入力信号の値のみが計算に使用されるこのようなフィルターは、単純または非再帰的と呼ばれます。 非再帰フィルター アルゴリズムは、フィルターのインパルス応答がわかっていれば簡単に作成できます。 アルゴリズムを実際に実装するには、インパルス応答に有限数の項が含まれている必要があります。 インパルス応答に無限数の項が含まれているものの、それらの値がすぐに減少する場合は、値が小さい項を破棄して有限数の項に制限することができます。 インパルス応答の要素の値が減少しない場合、非再帰フィルター アルゴリズムは実現不可能であることがわかります。
米。 4.4. -鎖 例として、 - 回路に似た最も単純なデジタル フィルターを考えてみましょう (図 4.4)。 回路のインパルス応答は次の形式になります。
対応するデジタル フィルターのインパルス応答を記述するには、次の式に置き換える必要があります。 ただし、回路のインパルス応答には次元があり、デジタル フィルターのインパルス応答は無次元でなければなりません。 したがって、式 (4.2) の乗数を省略し、デジタル フィルターのインパルス応答を次の形式で記述します。
このようなインパルス応答には無限に多くの項が含まれますが、その大きさは指数関数に従って減少するため、次のように選択して項を制限することができます。 これで、フィルター出力での信号の式を書くことができます。 この式もデジタル フィルター アルゴリズムです。 このフィルタの図を図に示します。 4.5. デジタル フィルターのプロセスを分析する 2 番目のアプローチは、従来のアナログ回路を分析するオペレーター法と似ていますが、ラプラス変換の代わりに - 変換が使用される点が異なります。
米。 4.5. -回路に類似した非再帰デジタルフィルターの回路 電気回路の伝達関数に似たデジタル フィルター パラメーターを定義してみましょう。 これを行うには、デジタル フィルターのインパルス応答に変換を適用します。
この機能をシステムフィルター機能と呼びます。 式 (4.1) によれば、デジタル フィルターの出力における信号は、入力信号とフィルターのインパルス応答の離散畳み込みに等しくなります。 この式に畳み込み定理を適用すると、出力信号変換は入力信号変換にシステム フィルター関数を乗算した値に等しいことがわかります。
したがって、システム関数はデジタル フィルターの伝達関数の役割を果たします。 例として、 - 回路に似た 1 次デジタル フィルターのシステム関数を見つけてみましょう。
デジタル フィルターを通過する信号を解析する 3 番目の方法は、古典的な微分方程式の方法に似ています。 オーダーチェーンを例としてこの方法を考えてみましょう。 1 次の最も単純なアナログ回路は - 回路 (図 4.4 を参照) であり、信号の通過は微分方程式で記述されます。
離散回路の場合、微分方程式 (4.8) の代わりに、入力信号と出力信号が離散時間で指定される差分方程式を作成する必要があり、微分の代わりに、隣接する信号値の差が表示されます。 離散 1 次回路の場合、差分方程式はかなり一般的な形式で書くことができます。 変換を方程式に適用してみましょう システムフィルター関数がある場所
式 (4.10) は、1 次デジタル フィルターのシステム関数のかなり一般的な式です。 先に求めたα回路に相当するデジタルフィルタのシステム関数の式(4.7)と一致する場合。 システム関数 (4.10) に対応するデジタル フィルタリング アルゴリズムを見つけてみましょう。 これを行うには、方程式 (4.9) を解きます。 このアルゴリズムの等価図を図に示します。 4.6. 非再帰フィルター (図 4.5 を参照) と比較して、ここでは一種の「フィードバック回路」が追加されています。これは、出力信号の値が後続のフィルターで使用されることを意味します。
米。 4.6. -回路に類似した再帰型デジタルフィルターの回路 計算。 このタイプのフィルターは再帰的と呼ばれます。 アルゴリズム (4.11) は、以前に検討した非再帰フィルターと完全に同等のフィルターに対応します。 ただし、非再帰フィルター アルゴリズム (4.4) を使用して出力信号の 1 つの値を決定するには、演算を実行する必要があります。再帰フィルター アルゴリズム (4.11) を使用する場合、必要な演算は 2 つだけです。 これが再帰的フィルターの主な利点です。 さらに、再帰フィルタを使用すると、インパルス応答の「テール」を破棄することなく、より正確にインパルス応答を実装できるため、より高精度の信号処理が可能になります。 再帰的フィルターを使用すると、非再帰的フィルターではまったく実装できないアルゴリズムを実装できます。 たとえば、図の回路に従って動作するフィルターを使用します。 4.6 は本質的に理想的なアキュムレータ/積分器であり、次の形式のインパルス応答を持ちます。このような特性を持つフィルタは、非再帰スキームを使用して実装することはできません。 検討した例は、長いインパルス応答を持つデジタル フィルターを作成するために非再帰アルゴリズムを使用することに意味がないことを示しています。 このような場合、再帰的フィルターを使用する方が適切です。 非再帰アルゴリズムの応用分野は、少数の項を含むインパルス応答を備えたデジタル フィルターの実装です。 例は、出力信号が入力信号の増分に等しい最も単純な微分器です。 このようなデジタルフィルターの回路を図に示します。 4.7.
米。 4.7. 最も単純なデジタル微分器の回路 ここで、次の方程式で表される一般的なデジタル フィルターについて考えてみましょう。 この方程式は、別の方法で書き直すと、次数の差分方程式としても、デジタル フィルター アルゴリズムとしても考えることができます。
米。 4.8. 再帰的デジタル次数フィルタ回路 アルゴリズム (4.13) は図に示す回路に対応します。 4.8. このようなフィルターのシステム関数を求めてみましょう。 これを行うには、方程式に変換を適用します。 式 (4.14) により、フィルタ回路の要素の変動とシステム機能との間の関係を確立することができます。 システム関数の分子の係数によって、次の係数の値が決まります。 (フィルターの非再帰部分)、分母の係数によってフィルターの再帰部分が決まります。 |




 .
.